• Preamble
  • Relaxation of Sequential Consistency
  • Introduction to candidate relaxations
  • More candidate relaxations
  • Summary of simple candidate relaxations
• Testing candidate relaxations with diy
  • Principle
  • Testing x86
• Additional relaxations
  • Intra-processor dependencies
  • Composite relaxations and cumulativity
• Identifying coherence orders with observers
  • Simple observers
  • More observers
  • Three stores or more
• Command usage
  • Usage of diyone
  • Usage of diy
  • Usage of readRelax

The authors of diy are Jade Alglave and Luc Maranget (INRIA Paris–Rocquencourt).

4  Preamble

We wrote diy as part of our empirical approach to studying relaxed memory models: developing in tandem testing tools and models of multiprocessor behaviour. In this tutorial, we attempt an independent tool presentation. Readers interested by the companion formalism are invited to refer to our CAV 2010 publication [1].

4.1  Relaxation of Sequential Consistency

Relaxation is one of the key concepts behind simple analysis of weak memory models. We define a candidate relaxation by reference to the most natural model of parallel execution in shared memory: Sequential Consistency (SC), as defined by L. Lamport [3]. A parallel program running on a sequentially consistent machine behaves as an interleaving of its sequential threads.

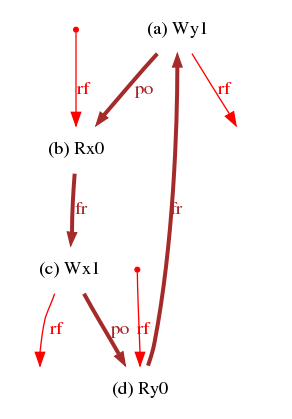
Consider once more the example classic.litmus:

X86 classic
"Fre PodWR Fre PodWR"
{ x=0; y=0; }
 P0          | P1          ; 
 MOV [y],$1  | MOV [x],$1  ; #(a)Wy1  | (c)Wx1
 MOV EAX,[x] | MOV EAX,[y] ; #(b)Rx0  | (d)Ry0
exists (0:EAX=0 /\ 1:EAX=0)

To focus on interaction through shared memory, let us consider memory accesses, or memory events. A memory event will hold a direction (write, written W, or read, written R), a memory location (written x, y) a value and a unique label. In any run of the simple example above, four memory events occur: two writes (c) Wx1 and (a) Wy1 and two reads (b) Rxv₁ with a certain value v₁ and (d) Ryv₂ with a certain value v₂.

If the program’s behaviour is modelled by the interleaving of its events, the first event must be a write of value 1 to location x or y and at least one of the loads must see a 1. Thus, a SC machine would exhibit only three possible outcomes for this test:

However, running (see Sec. 1.1) this test on a x86 machine yields an additional result:

And indeed, x86 allows each write-read pair on both processors to be reordered [2]: thus the write-read pair in program order is relaxed on each of these architectures. We cannot use SC as an accurate memory model for modern architectures. Instead we analyse memory models as relaxing the ordering constraints of the SC memory model.

4.2  Introduction to candidate relaxations

Consider again our classical example, from a SC perspective. We briefly argued that the outcome “0:EAX = 0 ∧ 1:EAX = 0” is forbidden by SC. We now present a more complete reasoning:

• From the condition on outcome, we get the values in read events: (b) Rx0 and (d) Ry0.
• Because of these values, (b) Rx0 must precede the write (c) Wx1 in the final interleaving of SC. Similarly, (d) Ry0 must precede the write (a) Wy1. This we note (b) →^fr (c) and (d) →^fr (a).
• Because of sequential execution order on one single processor (a.k.a. program order), (a) Wy1 must precede (b) Rx0 (first processor); while (c) Wx1 must precede (d) Ry0 (second processor). This we note (a) →^po (b) and (c) →^po (d).
• We synthesise the four constraints above as the following graph:
  
  Constraint arrows or global arrows are shown in brown colour. As the graph contains a cycle of brown arrows, the events cannot be ordered. Hence the execution presented is not allowed by SC.

The key idea of diy resides in producing programs from similar cycles. To that aim, the edges in cycles must convey additional information:

• For →^po edges, we consider whether the locations of the events on both sides of the edge are the same or not (’s’ or ’d’); and the direction of these events (W or R). For instance the two →^po edges in the example are PodWR. (program order edge between a write and a read whose locations are different).
• For →^fr edges, we consider whether the processor of the events on both sides of the edge are the same or not (’i’ for internal, or ’e’ for external). For instance the two →^fr edges in the example are Fre.

So far so good, but our x86 machine produced the outcome 0:EAX = 0 ∧ 1:EAX = 0. The Intel Memory Ordering White Paper [2] specifies: “Loads may be reordered with older stores to different locations”, which we rephrase as: PodWR is relaxed. Considering Fre to be safe, we have the graph:

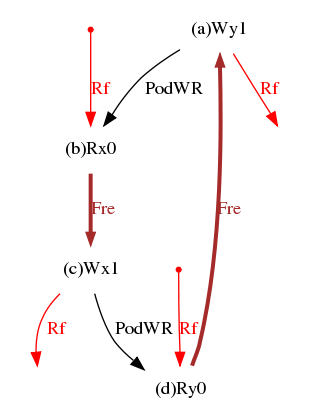
And the brown sub-graph becomes acyclic.

We shall see later why we choose to relax PodWR and not Fre. At the moment, we observe that we can assume PodWR to be relaxed and Fre not to be (i.e. to be safe) and test our assumptions, by producing and running more litmus tests. The diy suite precisely provides tools for this approach.

As a first example, classic.litmus can be created as follows:

% diyone -arch X86 -name classic Fre PodWR Fre PodWR

As a second example, we can produce several similar tests as follows:

% diy -arch X86 -safe Fre -relax PodWR -name classic
Generator produced 2 tests
Relaxations tested: {PodWR}

diy produces two litmus tests, classical000.litmus and classical001.litmus, plus one index file @all. One of the litmus tests generated is the same as above, while the new test is:

% cat classic001.litmus
X86 classic001
"Fre PodWR Fre PodWR Fre PodWR"
Cycle=Fre PodWR Fre PodWR Fre PodWR
Relax=PodWR
Safe=Fre
{ }
 P0          | P1          | P2          ;
 MOV [z],$1  | MOV [x],$1  | MOV [y],$1  ;
 MOV EAX,[x] | MOV EAX,[y] | MOV EAX,[z] ;
exists (0:EAX=0 /\ 1:EAX=0 /\ 2:EAX=0)
% cat @all
# diy -arch X86 -safe Fre -relax PodWR -name classic
# Revision: 3333
classic000.litmus
classic001.litmus

diy first generates cycles from the candidate relaxations given as arguments, up to a limited size, and then generates litmus tests from these cycles.

4.3  More candidate relaxations

We assume the memory to be coherent. Coherence implies that, in a given execution, the writes to a given location are performed by following a sequence, or coherence order, and that all processors see the same sequence.

In diy, the coherence orders are specified indirectly. For instance, the candidate relaxation Wse (resp. Wsi) specifies two writes, performed by different processors (resp. the same processor), to the same location ℓ, the first write preceding the second in the coherence order of ℓ. The condition of the produced test then selects the specified coherence orders. Consider for instance:

% diyone -arch X86 -name ws Wse PodWW Wse PodWW

The cycle that reveals a violation of the SC memory model is:

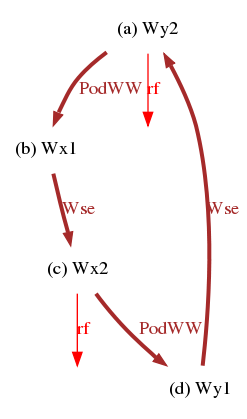
So the coherence order is 0 (initial store, not depicted), 1, 2 for both locations x and y. While the produced test is:

X86 ws "Wse PodWW Wse PodWW"
{ }
 P0         | P1         ;
 MOV [y],$2 | MOV [x],$2 ;
 MOV [x],$1 | MOV [y],$1 ;
exists (x=2 /\ y=2)

By the coherence hypothesis, checking the final value of locations suffices to characterise those two coherence orders, as expressed by the final condition of ws:

exists (x=2 /\ y=2)

See Sec. 7 for alternative means to identify coherence orders.

Candidate relaxations Rfe and Rfi relate writes to reads that load their value. We are now equipped to generate the famous iriw test (independent reads of independent writes):

% diyone -arch X86 Rfe PodRR Fre Rfe PodRR Fre -name iriw

We generate its internal variation (i.e. where all Rfe are replaced by Rfi) as easily:

% diyone -arch X86 Rfi PodRR Fre Rfi PodRR Fre -name iriw-internal

We get the cycles of Fig. 1,

---

Figure 1: Cycles for iriw and iriw-internal

---

and the litmus tests of Fig. 2.

---

Figure 2: Litmus tests iriw and iriw-internal

X86 iriw "Rfe PodRR Fre Rfe PodRR Fre" { } P0 | P1 | P2 | P3 ; MOV EAX,[y] | MOV [x],$1 | MOV EAX,[x] | MOV [y],$1 ; MOV EBX,[x] | | MOV EBX,[y] | ; exists (0:EAX=1 /\ 0:EBX=0 /\ 2:EAX=1 /\ 2:EBX=0)

X86 iriw-internal "Rfi PodRR Fre Rfi PodRR Fre" { } P0 | P1 ; MOV [x],$1 | MOV [y],$1 ; MOV EAX,[x] | MOV EAX,[y] ; MOV EBX,[y] | MOV EBX,[x] ; exists (0:EAX=1 /\ 0:EBX=0 /\ 1:EAX=1 /\ 1:EBX=0)

---

Candidate relaxations given as arguments really are a “concise specification”. As an example, we get iriw for Power, simply by changing -arch X86 into -arch PPC.

% diyone -arch PPC Rfe PodRR Fre Rfe PodRR Fre
PPC a
"Rfe PodRR Fre Rfe PodRR Fre"
{
0:r2=y; 0:r4=x;
1:r2=x;
2:r2=x; 2:r4=y;
3:r2=y;
}
 P0           | P1           | P2           | P3           ;
 lwz r1,0(r2) | li r1,1      | lwz r1,0(r2) | li r1,1      ;
 lwz r3,0(r4) | stw r1,0(r2) | lwz r3,0(r4) | stw r1,0(r2) ;
exists (0:r1=1 /\ 0:r3=0 /\ 2:r1=1 /\ 2:r3=0)

Also notice that without the -name option, diyone writes its result to standard output.

4.4  Summary of simple candidate relaxations

We summarise the candidate relaxations available on all architectures.

4.4.1  Communication candidate relaxations

We call communication candidate relaxations the relations between two events communicating through memory, though they could belong to the same processor. Thus, these events operate on the same memory location.

4.4.2  Program order candidate relaxations

We call program order candidate relaxations each relation between two events in the program order. These events are on the same processor, since they are in program order. As regards code output, diy interprets a program order candidate relaxation by generating two memory instructions (load or store) following one another.

Program order candidate relaxations have the following syntax:

where:

• s (resp. d) indicates that the two events are to the same (resp. different) location(s);
• R (resp. W) indicates an event to be a read (resp. a write);

In practice, we have:

It is to be noticed that PosWR, PosWW and PosRW are similar to Rfi, Wsi and Fri, respectively. More precisely, diy is unable to consider a PosWR (or PosWW, or PosRW) candidate relaxation as not being also a Rfi (or Wsi, or Fri) candidate relaxation. However, litmus tests conditions may be more informative in the case of Rfi and Fri.

4.4.3  Fence candidate relaxations

Relaxed architectures provide specific instructions, namely barriers or fences, to enforce order of memory accesses. In diy the presence of a fence instruction is specified with fence candidate relaxations, similar to program order candidate relaxations, except that a fence instruction is inserted. Hence we have FencedsRR, FenceddRR. etc. The inserted fence is the strongest fence provided by the architecture — that is, mfence for x86 and sync for Power.

Fences can also be specified by using specific names. More precisely, we have MFence for x86; while on Power we have Sync and LwSync. Hence, to yield two reads to different locations and separated by the lightweight Power barrier lwsync, we specify LwSyncdRR.

5  Testing candidate relaxations with diy

Teh tool diy can probably be used in various, creative, ways; but the tool first stems from our technique for testing relaxed memory models. The -safe and -relax options are crucial here. We describe our technique by the means of an example: X86-TSO.

5.1  Principle

Before engaging in testing it is important to categorise candidate relaxations as safe or relaxed.

This can done by interpretation of vendor’s documentation. For instance, the iriw test of Sec. 4.3 is the example 7.7 of [2] “Stores Are Seen in a Consistent Order by Other Processors”, with a Forbid specification. Hence we deduce that Fre, Rfe and PodRR are safe. Then, from test iriw-internal of Sec. 4.3, which is Intel’s test 7.5 “Intra-Processor Forwarding Is Allowed” with an allow specification, we deduce that Rfi is relaxed. Namely, the cycle of iriw-internal is “Fre Rfi PodRR Fre Rfi PodRR”. Therefore, the only possibility is for Rfi to be relaxed.

Overall, we deduce:

• Candidate relaxations PosWR (Rfi) and PodWR are relaxed
• The remaining candidate relaxations PosRR, PodRR, PosWW (Wsi), PodWW, PosRW (Fri), Fre and Wse are safe. Fence relaxations FencedsWR and FenceddWR are also safe and worth testing.

Of course these remain assumptions to be tested. To do so, we perform one series of tests per relaxed candiate relaxation, and one series of tests for confirming safe candidate relaxations as much as possible. Let S be all safe candidate relaxations.

• Let r be a relaxed candidate relaxation. We produce tests for confirming r being relaxed by diy -relax r -safe S. We run these tests with litmus. If one of the tests yields Ok, then r is confirmed to be relaxed, provided the experiments on S below do not fail.
• For confirming the safe set, we produce tests by diy -safe S. We run these tests as much as possible and expect never to see Ok.

Namely, diy builds cycles as follows:

• diy -relax r -safe S build cycles with at least one r taking other candidate relaxations from S.
• diy -safe S build cycles from the candidate relaxations in S.

For the purpose of confirming relaxed candidate relaxations, S can be replaced by a subset.

5.2  Testing x86

Repeating command line options is painful and error prone. Besides, configuration parameters may get lost. Thus, we regroup those in configuration files that simply list the options to be passed to diy, one option per line. For instance here is the configuration file for testing the safe relaxations of x86, x86-safe.conf.

#safe x86 conf file
-arch X86
#Generate tests on four processors or less
-nprocs 4
#From cycles of size at most six
-size 6
#With names safe000, safe0001,...
-name safe
#List  of safe relaxations
-safe PosR* PodR* PodWW PosWW Rfe Wse Fre FencedsWR FenceddWR 

Observe that the syntax of candidate relaxations allows one shortcut: the wildcard * stands for W and R. Thus PodR* gets expanded to the two candidate relaxations PodRR and PodRW.

We get safe tests by issuing the following command, preferably in a specific directory, say safe.

% diy -conf x86-safe.conf
Generator produced 38 tests
Relaxations tested: {}

Here are the configuration files for confirming that Rfi and PodWR are relaxed, x86-rfi.conf and x86-podwr.conf.

#rfi x86 conf file
-arch X86
-nprocs 4
-size 6 
-name rfi
-safe PosR* PodR* PodWW PosWW Rfe Wse Fre FencedsWR FenceddWR 
-relax Rfi

#podrw x86 conf file
-arch X86
-nprocs 4
-size 6
-name podwr
-safe Fre
-relax PodWR

Notice that we used the complete safe list in x86-rfi.conf and a reduced list in x86-podwr.conf. Tests are to be generated in specific directories. To that aim, we provide a convenient archive x86.tar.

% cd rfi
% diy -conf x86-rfi.conf 
Generator produced 11 tests
Relaxations tested: {Rfi}
% cd ../podwr
% diy -conf x86-podwr.conf 
Generator produced 2 tests
Relaxations tested: {PodWR}
% cd ..

Now, let us run all tests at once, with the parameters of machine saumur (4 physical cores with hyper-threading):

% litmus -mach saumur rfi/@all > rfi/saumur.rfi.00
% litmus -mach saumur podwr/@all > podwr/saumur.podwr.00
% litmus -mach saumur safe/@all > safe/saumur.safe.00

If your machine has 2 cores only, try litmus -a 2 -limit true…

We now look for the tests that have validated their condition in the result files of litmus. A simple tool, readRelax, does the job:

% readRelax rfi/saumur.rfi.00 podwr/saumur.podwr.00 safe/saumur.safe.00
   .
   .
   .
** Relaxation summary **
{Rfi} With {Rfe, Fre, Wse, PodRW, PodRR} {Rfe, Fre, PodRR}\
{Fre, Wse, PodWW, PodRR} {Fre, PosWW, PodRR, MFencedWR}\
{Fre, PodWW, PodRR, MFencedWR} {Fre, PodRR} {Fre, PodRR, MFencedWR}
{PodWR} With {Fre}

The tool readRelax first lists the result of all tests (which is omitted above), and then dumps a summary of the relaxations it found. The sets of the candidate relaxations that need to be safe for the tests to indeed reveal a relaxed candidate relaxation are also given. Here, Rfi and PodWR are confirmed to be relaxed, while no candidate relaxation in the safe set is found to be relaxed. Had it been the case, a line {} With {...} would have occurred in the relaxation summary. The safe tests need to be run a lot of times, to increase our confidence in the safe set.

6  Additional relaxations

We introduce some additional candidate relaxations that are specific to the Power architecture. We shall not detail here our experiments on Power machines. See our experience report http://diy.inria.fr/phat/ for more details.

6.1  Intra-processor dependencies

In a very relaxed architecture such as Power, intra-processor dependencies becomes significant. Roughly, intra-processor dependencies fall into two categories:

Data dependencies

occur when a memory access instruction reads a register whose contents depends upon a previous (in program order) load. In diy we specify such a dependency as:

Dp(s|d)(R|W)

where, as usual, s (resp. d) indicates that the source and target events are to the same (resp. different) location(s); and R (resp. W) indicates that the target event is a read (resp. a write). As a matter of fact, we do not need to specify the direction of the source event, since it always is a read.

Control dependencies

occur when the execution of a memory access is conditioned by the contents of a previous load. Their syntax is similar to the one of Dp relaxations, with a Ctrl tag:

Ctrl(s|d)(R|W)

In the produced code, diy expresses a data dependency by a false dependency (or dummy dependency) that operates on the address of the target memory access. For instance:

% diyone DpdW Rfe DpdW Rfe
PPC a "DpdW Rfe DpdW Rfe"
{ 0:r2=x; 0:r5=y; 1:r2=y; 1:r5=x; }
 P0            | P1            ;
 lwz r1,0(r2)  | lwz r1,0(r2)  ;
 xor r3,r1,r1  | xor r3,r1,r1  ;
 li r4,1       | li r4,1       ;
 stwx r4,r3,r5 | stwx r4,r3,r5 ;
exists (0:r1=1 /\ 1:r1=1)

On P₀, the effective address of the indexed store stwx r4,r3,r5 depends on the contents of the index register r3, which itself depends on the contents of r1. The dependency is a “false” one, since the contents of r3 always is zero, regardless of the contents of r1.

A control dependency is implemented by the means of an useless compare and branch sequence, plus the isync instruction when the target event is a load. For instance

% diyone CtrldR Fre SyncdWW Rfe
PPC a
"CtrldR Fre SyncdWW Rfe"
{ 0:r2=x; 0:r4=y; 1:r2=y; 1:r4=x; }
 P0           | P1           ;
 li r1,1      | lwz r1,0(r2) ;
 stw r1,0(r2) | cmpw r1,r1   ;
 sync         | beq  LC00    ;
 li r3,1      | LC00:        ;
 stw r3,0(r4) | isync        ;
              | lwz r3,0(r4) ;
exists (1:r1=1 /\ 1:r3=0)

Of course, in both cases, we assume that dependencies are not “optimised out” by the assembler or the hardware.

6.2  Composite relaxations and cumulativity

Users may specify a small sequence of single candidate relaxations as behaving as a single candidate relaxation to diy. The syntax is:

The main usage of the feature is to specify cumulativity candidate relaxations, that is, the sequence of Rfe and of a fence candidate relaxation (A-cumulativity), the sequence of a fence candidate relaxation and of Rfe (B-cumulativity), or both (AB-cumulativity).

Cumulativity candidate relaxations are best expressed by the following syntactical shortcuts: let r be a fence candidate relaxation, then ACr stands for [Rfe,r], BCr stands for [r,Rfe], while ABCr stands for [Rfe,r,Rfe],

Hence, a simple way to generate iriw-like (see Sec. 4.3) litmus tests with lwsync is as follows:

% diy -name iriw-lwsync -nprocs 8 -size 8 -relax ACLwSyncdRR -safe Fre
Generator produced 3 tests
Relaxations tested: {ACLwSyncdRR}

where we have for instance:

% cat iriw-lwsync001.litmus 
PPC iriw-lwsync001
"Fre Rfe LwSyncdRR Fre Rfe LwSyncdRR Fre Rfe LwSyncdRR"
Cycle=Fre Rfe LwSyncdRR Fre Rfe LwSyncdRR Fre Rfe LwSyncdRR
Relax=ACLwSyncdRR
Safe=Fre
{
0:r2=z; 0:r4=x; 1:r2=x;
2:r2=x; 2:r4=y; 3:r2=y;
4:r2=y; 4:r4=z; 5:r2=z;
}
 P0           | P1           | P2           | P3           | P4           | P5           ;
 lwz r1,0(r2) | li r1,1      | lwz r1,0(r2) | li r1,1      | lwz r1,0(r2) | li r1,1      ;
 lwsync       | stw r1,0(r2) | lwsync       | stw r1,0(r2) | lwsync       | stw r1,0(r2) ;
 lwz r3,0(r4) |              | lwz r3,0(r4) |              | lwz r3,0(r4) |              ;
exists (0:r1=1 /\ 0:r3=0 /\ 2:r1=1 /\ 2:r3=0 /\ 4:r1=1 /\ 4:r3=0)

7  Identifying coherence orders with observers

We first produce the “four writes” test W4 for Power:

% diyone -name W4 -arch PPC PodWW Wse PodWW Wse
% cat W4.litmus
PPC W4
"PodWW Wse PodWW Wse"
{ 0:r2=x; 0:r4=y; 1:r2=y; 1:r4=x; }
 P0           | P1           ;
 li r1,2      | li r1,2      ;
 stw r1,0(r2) | stw r1,0(r2) ;
 li r3,1      | li r3,1      ;
 stw r3,0(r4) | stw r3,0(r4) ;
exists (x=2 /\ y=2)

Test W4 is the Power version of X86 test ws of Sec. 4.3. In that section, we argued that the final condition exists (x=2 /\ y=2) suffices to identify the coherence orders 0, 1, 2 for locations x and y. As a consequence, a positive final condition reveals the occurrence of the specified cycle: Wse PodWW Wse PodWW.

7.1  Simple observers

Observers provide an alternative, perhaps more intuitive, means to identify coherence orders: an observer simply is an additional thread that performs several loads from the same location in sequence. Here, loading value 1 and then value 2 from location x identifies the coherence order 0, 1, 2. The command line switch -obs force commands the production of observers (test W4Obs):

% diyone -name W4Obs -obs force -obstype straight -arch PPC PodWW Wse PodWW Wse
% cat W4Obs.litmus
PPC W4Obs
"PodWW Wse PodWW Wse"
{ 0:r2=x; 1:r2=y; 2:r2=x; 2:r4=y; 3:r2=y; 3:r4=x; }
 P0           | P1           | P2           | P3           ;
 lwz r1,0(r2) | lwz r1,0(r2) | li r1,2      | li r1,2      ;
 lwz r3,0(r2) | lwz r3,0(r2) | stw r1,0(r2) | stw r1,0(r2) ;
              |              | li r3,1      | li r3,1      ;
              |              | stw r3,0(r4) | stw r3,0(r4) ;
exists (0:r1=1 /\ 0:r3=2 /\ 1:r1=1 /\ 1:r3=2)

Thread P0 observes location x, while thread P1 observes location x. With respect to W4, final condition has changed, the direct observation of the final contents of locations x and y being replaced by two successive observations of the contents of x and y.

It should first be noticed that the reasoning above assumes that having the same thread to read 1 from say x and then 2 implies that 1 takes place before 2 in the coherence order of x. This need not be the case in general — although it holds for Power. Moreover, running W4 and W4Obs yields contrasted results. While a positive conclusion is immediate for W4, we were not able to reach a similar conclusion for W4Obs. As a matter of fact, W4Obs yielding Ok stems from the still-to-be-observed coincidence of several events: both observers threads must run at the right pace to observe the change from 1 to 2, while the cycle must indeed occur.

7.2  More observers

A simple observer consisting of loads performed in sequence is a straight observer. We define two additional sorts of observers: fenced observers, where loads are separated by the strongest fence available, and loop observers, which poll on location contents change. Those are selected by the homonymous tags given as arguments to the command line switch -obstype. For instance, we get the test W4ObsFenced by:

% diyone -name W4ObsFenced -obs force -obstype fenced -arch PPC PodWW Wse PodWW Wse
% cat W4ObsFenced.litmus
PPC W4ObsFenced
"PodWW Wse PodWW Wse"
{ 0:r2=x; 1:r2=y; 2:r2=x; 2:r4=y; 3:r2=y; 3:r4=x; }
 P0           | P1           | P2           | P3           ;
 lwz r1,0(r2) | lwz r1,0(r2) | li r1,2      | li r1,2      ;
 sync         | sync         | stw r1,0(r2) | stw r1,0(r2) ;
 lwz r3,0(r2) | lwz r3,0(r2) | li r3,1      | li r3,1      ;
              |              | stw r3,0(r4) | stw r3,0(r4) ;
exists (0:r1=1 /\ 0:r3=2 /\ 1:r1=1 /\ 1:r3=2)

Invoking diyone as “diyone -obs force -obstype loop ...” yields the additional test W4ObsLoop:

PPC W4ObsLoop
"PodWW Wse PodWW Wse"
{ 0:r2=x; 1:r2=y;
  2:r2=x; 2:r4=y; 3:r2=y; 3:r4=x; }
 P0            | P1            | P2           | P3           ;
 L00:          | L03:          | li r1,2      | li r1,2      ;
 lwz r1,0(r2)  | lwz r1,0(r2)  | stw r1,0(r2) | stw r1,0(r2) ;
 cmpwi r1,0    | cmpwi r1,0    | li r3,1      | li r3,1      ;
 beq  L00      | beq  L03      | stw r3,0(r4) | stw r3,0(r4) ;
 li r4,200     | li r4,200     |              |              ;
 L01:          | L04:          |              |              ;
 lwz r3,0(r2)  | lwz r3,0(r2)  |              |              ;
 cmpw r3,r1    | cmpw r3,r1    |              |              ;
 bne  L02      | bne  L05      |              |              ;
 addi r4,r4,-1 | addi r4,r4,-1 |              |              ;
 cmpwi r4,0    | cmpwi r4,0    |              |              ;
 bne  L01      | bne  L04      |              |              ;
 L02:          | L05:          |              |              ;
exists (0:r1=1 /\ 0:r3=2 /\ 1:r1=1 /\ 1:r3=2)

A loop observer first busily waits for the observed location not to hold its initial contents 0, and then busily waits for another change of location contents. The second loop is performed at most a finite number of times (here 200), in order to ensure termination.

As an indication of the performance of the various sorts of observers, the following table summarises a litmus experiment performed on a 4-cores 2-ways SMT Power6 machine— complete litmus log.

The first row “Positive” shows the number of observed positive outcomes/total number of outcomes produced. The second row “(Final) States” shows the number of different outcomes observed in practice/theoretical value. For instance, in the case of W4, we observed the positive outcome x=2 /\ y=2 about 29 thousands times out of a total of 400 millions outcomes. Moreover, there are four possible outcomes: x=1 /\ y=1, x=1 /\ y=2, x=2 /\ y=1 and x=2 /\ y=2, which we all observed at least once. As a conclusion, all techniques achieve decent results, except straight observers.

7.3  Three stores or more

In test W4 the coherence orders sequence two writes. If there are three writes or more to the same location, it is no longer possible to identify a coherence order by observing the final contents of the memory location involved. In other words, observers are mandatory.

The argument to the -obs switch commands the production of observers. It can take three values:

accept

Produce observers when absolutely needed. More precisely, given memory location x, no equality on x appears in the final condition for zero or one write to x, one such appears for two writes, and observers are produced for three writes or more.

avoid

Never produce observers, i.e. fail when there are three writes to the same location.

force

Produce observers for two writes or more.

With diyone, one easily build a three writes test as for instance the following W5:

% diyone -obs accept -obstype fenced -arch PPC -name W5 Wse Wse PodWW Wse PodWW
% cat W5.litmus
PPC W5
"Wse Wse PodWW Wse PodWW"
{ 0:r2=y; 1:r2=y; 1:r4=x; 2:r2=x; 2:r4=y; 3:r2=y; }
 P0           | P1           | P2           | P3           ;
 lwz r1,0(r2) | li r1,3      | li r1,2      | li r1,2      ;
 sync         | stw r1,0(r2) | stw r1,0(r2) | stw r1,0(r2) ;
 lwz r3,0(r2) | li r3,1      | li r3,1      |              ;
 sync         | stw r3,0(r4) | stw r3,0(r4) |              ;
 lwz r4,0(r2) |              |              |              ;
exists (x=2 /\ 0:r1=1 /\ 0:r3=2 /\ 0:r4=3)

As apparent from the code above, we have a fenced observer thread on y (P0), while the final state of x is observed directly (x=2). The command line switch -obs force would yield two observers, while -obs avoid would lead to failure.

8  Command usage

The diy suite consists in three tools:

diyone

generates one litmus test from the specification of a violation of the sequential consistency memory model as a cycle—see Sec. 4.2.

diy

generates several tests, aimed confirming that candidate relaxations are relaxed or safe—see Sec. 5.

readRelax

Extract relevant information from the results of tests—see Sec. 5.2.

8.1  Usage of diyone

diyone takes a list of candidate relaxations as arguments and outputs a litmus test. Note that diyone may fail to produce the test, with a message that briefly details the failure.

% diyone Rfe Rfe PodRR
Test a [Rfe Rfe PodRR] failed:
Impossible direction PodRR Rfe

diyone accepts the following documented options.

-v

Be verbose, repeat to increase verbosity.

-version

Show version number and exit.

-obs <accept|avoid|force>

Management of observers, default is avoid. See Sec. 7.3.

-obstype <fenced|loop|straight>

Style of observers, default is fenced. See Sec. 7.2.

-optcond

Optimise conditions by disregarding the values of loads that are neither the target of Rf, nor the source of Fr. This is the default.

-nooptcond

Do not optimise conditions.

-name <name>

Set the name of the test to <name> and output it into file <name>.litmus. By default, the test name is a and output goes to standard output.

-arch <X86|PPC>

Set architecture. Default is PPC.

8.2  Usage of diy

The tool diy accepts the same options as diyone, option -name <name> being mandatory and setting the base name of generated litmus tests: i.e. diy produces tests <name>000, <name>001, etc., in files with extension .litmus. Moreover, diy produces an index file @all that lists file names <name>000.litmus, <name>001.litmus etc.

diy also accepts the following, additional, documented options.

-conf <file>

Read configuration file <file>. A configuration file consists in a list of options, one option per line. Lines introduced by # are comments and are thus ignored.

-o <name.tar>

Output litmus tests as an archive <name.tar>. The default is to output them in the current directory.

-size <n>

Set the maximal size of cycles. Default is 6.

-exact

Produce cycles of size exactly <n>, in place of size up to <n>.

-nprocs <n>

Reject tests with more than <n> threads. Default is 4.

-eprocs

Produce tests with exactly <n> threads, where <n> is set above.

-ins <n>

Reject tests as soon as the code of one thread consists of more than <n> instructions. Default is 4.

-c <bool>

Avoid equivalent cycles. Default is true.

-relax <relax-list>

Set relax list. Default is empty. The syntax of <relax-list> is a comma (or space) separated list of candidate relaxations.

-mix <bool>

Mix the elements of the relax list (see below), default false.

-maxelax <n>

In mix mode, upper bound on the number of different candidate relaxations tested together. Default is 100.

-safe <relax-list>

Set safe list. Default is empty.

-mode <critical|sc>

Control generation of cycles, default sc. Critical mode offers predictive control on cycle generation (see below), and is activated when diy is invoked by the automated front-end dont.

-cumul <bool>

Permit implicit cumulativity, i.e. authorise building up the sequence Rfe followed by a fence, or the reverse. Default is true.

The relax and safe lists command the generation of cycles as follows:

1. When the relax list is empty, cycles are built from the candidate relaxations of the safe list.
2. When the relax list is of size 1, cycles are built from its single element r and from the elements of the safe list. Additionally, the cycle produced contains r at least once.
3. When the relax list is of size n, with n > 1, the behaviour of diy depends on the mix mode:
   1. By default (-mix false), diy generates n independent sets of cycles, each set being built with one relaxation from the relax list and all the relaxations in the safe list. In other words, diy on a relax list of size n behaves similarly to n runs of diy on each candidate relaxation in the list.
   2. Otherwise (-mix true), diy generates cycles that contains at least one element from the relax list, including some cycles that contain different relaxations from the relax list. The cycles will contain at most m different elements from the relax list, where m is specified with option “-maxrelax m”.

Generally speaking, diy generates “some” cycles and does not generate “all” cycles (up to a certain size e.g.). In (default) sc mode, diy performs some optimisation, most of which we leave unspecified. As an exception to this non-specification, diy is guaranteed not to generate redundant elementary communication relaxation in the following sense: let us call Com the union of Ws, Rf and Fr (the e|i specification is irrelevant here). Ws being transitive and by definition of Fr, one easily shows that the transitive closure Com+ of Com is the union of Com plus [Ws,Rf] (Ws followed by Rf) plus [Fr,Rf]. As a consequence, maximal subsequences of communication relaxations in diy cycles are limited to single relaxations (i.e. Ws, Rf and Fr) and to the hereabove mentioned two sequences (i.e. [Ws,Rf] and [Fr,Rf]). For instance, [Ws,Ws] and [Fr,Ws] should never appear in diy generated cycles. However, such subsequences can be generated on an individual basis with diyone, see the example of W5 in Sec 7.3.

In critical mode (-mode critical), cycles are strictly specified as follows:

1. Communication candidate relaxations sequences are limited to Rf,Fr,Ws,[Ws,Rf] and [Fr,Rf], as in sc mode.
2. No two internal² candidate relaxations follow one another.
3. If the option -cumul false is specified, diy will not construct the sequence of Rfe followed by a fence (or B-cumulativity) candidate relaxation or of a fence (or A-cumulativity) candidate relaxation followed by Rfe.
4. None of the rules above applies to the internal sequences of composite candidate relaxations. For instance, if [Rfi,PodRR] is given as a candidate relaxation, the sequence “Rfi,PodRR” appears in cycles.

The cycles described above are the critical cycles of [4].

8.3  Usage of readRelax

readRelax is a simple tool to extract relevant information out of litmus run logs. For a given run of a given litmus test, the relevant information is:

• Whether the test yielded Ok or not,
• An optional candidate relaxation, which is the one given as argument to diy option -relax at test build time, or none.
• The safe list relevant to the given test, i.e. the safe candidate relaxations that appear in the tested cycle.

See Sec. 5.2 for an example.

The tool readRelax takes file names as arguments. If no argument is present, it reads a list of file names on standard input, one name per line.

2

That is, the source and target accesses are by the same processor.