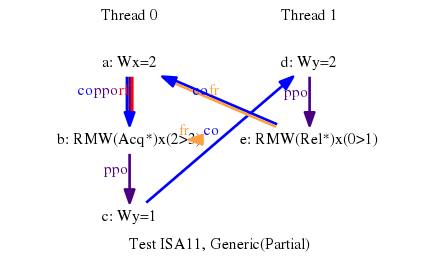
Illustration of a cornercase relative to the atomicity axiom in the total order formulation.
Although the store g lies between the read b and the store c in all valid global memory order, the test is allowed. This is due to store a lying between g and c.Let “<” be a valid global memory order, we show that we must have b < g < a < c.
-
We first have a < c, as the final value of x is written by c.
- Furthermore, b < d (b is a read-acquire), d < e (the final value
of y is written by e) and e < g (g is a write-release). Thus,
we have b < g by transitivity.
- Now, let us consider the relative positions of the writes g and a.
We cannot have a < g: if so, as b < g (see above),
we would contradict the atomicity axiom. Hence we must have g < a,
as “<” is a total order.
- We conclude b < g < a < c.
Allow.
RISCV ISA11
{
uint64_t x;
uint64_t y;
0:s0=x; 0:s1=y;
1:s0=x; 1:s1=y;
}
P0 | P1 ;
li t1,2 | li t3,2 ;
li t2,1 | li t4,1 ;
sd t1,0(s0) | sd t3,0(s1) ;
amoor.d.aq a0,t2,(s0) | amoswap.d.rl x0,t4,(s0) ;
sd t2,0(s1) | ;
exists 0:a0=2 /\ x=3 /\ y=2

